Исследование итеративного алгоритма декодирования MAP и разработка модели турбокодека в сиcтеме MathCAD

На сегодня турбокоды получили широкое распространение в области связи, особенно в технологиях беспроводной связи, таких как WiMAX, мобильные и спутниковые сети и др. Турбокоды особенно эффективны в каналах с низким отношением сигнал/шум, поэтому имеют огромные перспективы для использования в новых поколениях связи [4]. В этой статье представлен принцип работы турбокода и его итеративного декодирования при помощи алгоритма MAP. Также представлен численный пример кодирования и декодирования турбокода. Модель выполнена в среде MathCAD v.15, разработаны функции для вычисления всех параметров декодирования.

Структура 1/3 турбокодера показана на рисунке 1. Используем два идентичных свёрточных кодера. На первый поступает информационный бит , на второй поступает перемеженный информационный бит. В результате получаем один информационный бит и два проверочных. Для перемежения входной информационной последовательности используется псевдослучайный перемежитель (interleaver) [1; 5].

Рисунок 1. Структурная схема турбокодера

Каждый свёрточный кодер является систематическим рекурсивным RSC-кодером, но поскольку мы уже передаем информационный элемент  на выход турбокодера, то на выходе каждого из двух RSC-кодеров будут только проверочные элементы и .

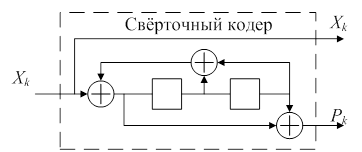
Рисунок 2. Схема RSC-кодера

При детектировании значения принятого символа из канала необходимо определить его значение функции правдоподобия. Расположение этого символавдоль оси х не позволяет однозначно определить значение передаваемого бита, поскольку в любой точке на оси х соответствуют два значения правдоподобия – для  и для . Основываясь на принципах жесткого решения и максимального правдоподобия, приемник должен сравнить значения  и  и вынести решение о принятом бите. Таким образом, в жесткой схеме принятия решения, при расположении точки правее порога x = 0, сигнал переносит бит «1».

Рисунок 3. Функции распределения вероятностей принятого сигнала

Если взять логарифм отношения  к  для a и b, то:

,

Как видно, вероятнее всего a является «0», а b является «1». Логарифм отношения  к  называется логарифмическим отношением функций правдоподобия (LLR – Log-Likelyhood Ratio).

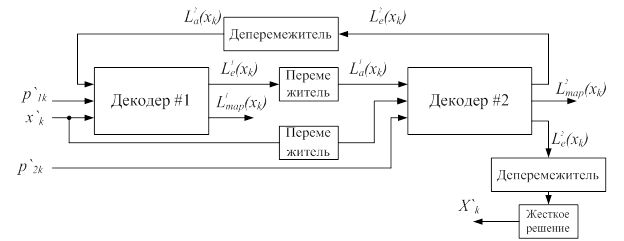
Рисунок 4. Структурная схема турбодекодера

MAP – это алгоритм декодирования по методу максимума апостериорной вероятности контролирующих ошибки кодов, определённых на решётках [5]. На рисунке 5 приведена блок-схема алгоритма MAP турбодекодера.

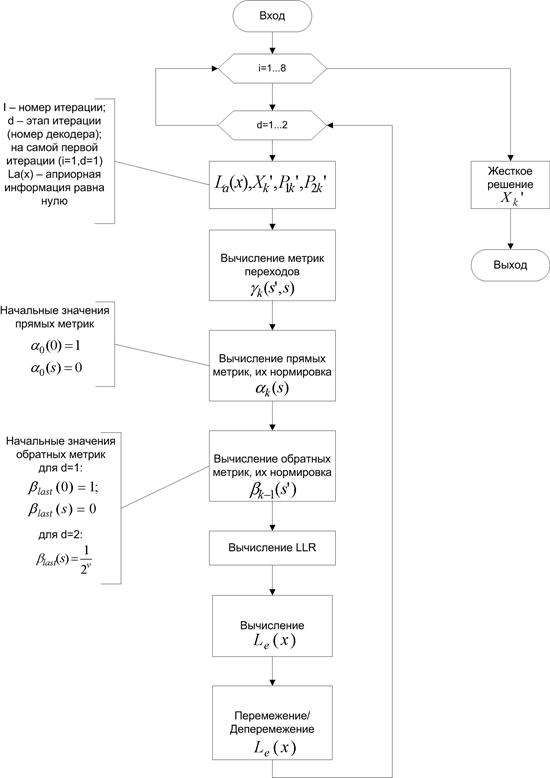
Рисунок 5. Блок-схема алгоритма MAP турбодекодера

Для вычисления LLR нужно рассчитать значения переходов между узлами решетки, прямую и обратную метрики. Переходы между узлами решетки рассчитываются как:

,

где:  и  – прошлое и следующее состояния, и  – информационный и проверочный символы на решетке, и  – информационный и проверочный символы на входе декодера, – качество канала, – информация с прошлой итерации работы декодера, k – номер элемента. Рассчитать прямую метрику α можно рекурсивно:

Расчет обратной метрики β так же вычисляется рекурсивно, начиная с конца решетки:

Чтобы начать вычисление метрик, нам нужно инициализировать начальные состояния:

Так как мы не знаем в каком состоянии остановлен свёрточный декодер #2, то его начальные значения β будут равны: , где  – количество ячеек в регистре памяти кодера. При этом результаты вычисления метрик нужно пронормировать: 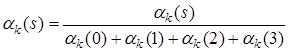 и .
Расчет LLR с выхода декодера осуществляется по формуле:

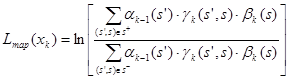
где:  – это априорная информация, которая является мягким выходом декодера после одной итерации декодирования,  – это внешняя информация, взятая из результата предыдущей итерации декодирования [6; 9].

Рассмотрим пример итеративного декодирования турбокода алгоритмом MAP [6]. На вход турбокодера отправим последовательность из шести битов:. Эти биты приходят на RSC #1. Результат кодирования показан на решетке:

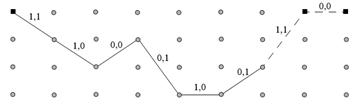
Рисунок 6. Кодирование в RSC #1

Искусственно остановим состояние решетки в нулевом состоянии, отправив дополнительно еще два бита:. Теперь перемежим эту информационную последовательность (с учётом добавочных битов) для отправки на второй декодер. Результат кодирования для RSC #2 и схема работы псевдослучайного перемежителя:

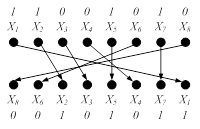
Рисунок 7. Кодирование в RSC #2 (слева) и схема работы перемежителя (справа)

Далее информационные и проверочные биты преобразуются в символы отправляются в канал. После этого получаем искаженную последовательность:

Таблица 1.

Передача информации по каналу с шумом

Первый этап первой итерации декодирования. Вычислим значение  при .

Таблица 2.

Переходы между узлами решетки

Таблица 3.

Результаты  с учетом нормировки

Таблица 4.

Результаты  с учетом нормировки

Результаты расчета LLR первого этапа первой итерации декодирования и расчет внешней информации для следующего декодера. Как видим, здесь три ошибки при декодировании:

Таблица 5.

Результаты первого этапа первой итерации

Второй этап первой итерации декодирования.

Таблица 6.

Переходы между узлами решетки

Таблица 7.

Результаты  с учетом нормировки

Таблица 8.

Результаты  с учетом нормировки

Результаты расчета LLR второго этапа первой итерации декодирования и расчет внешней информации для следующей итерации:

Таблица 9.

Результаты второго этапа первой итерации

Произведем обратное перемежение выхода второго этапа первой итерации декодирования  и примем жесткое решение:

Таблица 10.

Вывод результатов после декодеров

Декодер исправил ошибки. Мы можем произвести еще несколько итераций декодирования для увеличения доверия к полученным результатам. Результаты восьми этапов декодирования для четырех итераций:

Таблица 11.

Результаты 8 этапов декодирования

Количество итераций может быть разным для разных алгоритмов турбодекодирования. Это также зависит от параметров канала. Обычно если дальнейшее итеративное вычисление не приводит к смене знака выходной надежности бит, то утверждают, что декодер сошелся, т.е. пришел к некоторому стационарному состоянию [2; 3]. В данной работе принято вычислять 8 итераций. Существует три критерия остановки декодера. Подробно можно узнать в [7; 8].

В результате работы получена модель турбокодека в среде MathCAD, которую можно использовать для изучения процессов итеративного декодирования, изменения и создания модели для других алгоритмов работы турбокодов. Турбокоды имеют высокий потенциал и энергетическую эффективность, что позволяет их использовать в системах связи для увеличения дальности приема, скрытности системы, поэтому актуальность исследования итеративных кодов только возрастает.