Решение задачи прогнозирования при помощи использования нечеткой нейронной продукционной сети Ванга-Менделя

В данной работе для решения задачи прогнозирования выбрана нечеткая нейронная продукционная сеть Ванга-Менделя [1]. Данная сеть представляет собой четырехслойную структуру (рисунок 1), в которой первый слой отвечает за фуззификацию входных переменных, второй – агрегирует значения отдельных переменных  в условии i-го правила вывода, третий (линейный) – агрегирует M правил вывода (первый нейрон) и генерирует нормализующий сигнал (второй нейрон), а выходной слой (состоящий из одного нейрона) осуществляет нормализацию (формируя выходной сигнал y(x)).

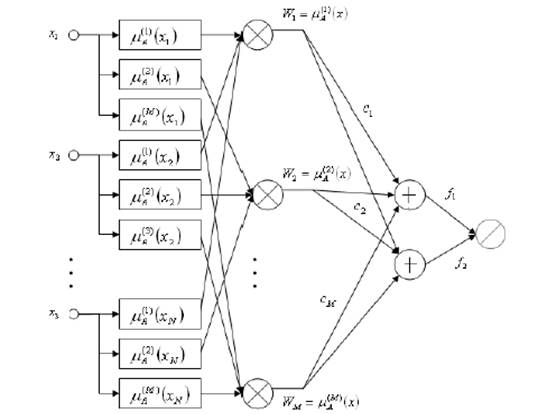
Рисунок 1. Структура нечеткой нейронной сети Ванга-Менделя

В этой структуре первый и третий слои - параметрические. В первом слое это параметры функции фуззификации  а в третьем слое - веса , интерпретируемые как центры  (функции принадлежности следствия i -того нечеткого правила вывода).

Роль фуззификатора играет обобщенная гауссовская функция:

Реализуемая вышеописанной четырехслойной структурой функция аппроксимации, с учетом введенных обозначений может быть представлена в виде:

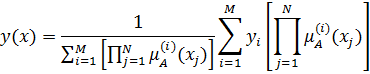
Для обучения нейронной сети был использован адаптивный алгоритм, сформулированный только для гауссовской функции (b = 1) с использованием обобщенной модели Ванга-Менделя. В результате его реализации определяются: количество центров кластеров а также их расположение в части, соответствующей условиям (множество векторов х_t) и заключениям (множество скалярных ожидаемых значений d_t). То есть, пространство данных разделяется на M кластеров, при этом мощность каждого из них определяется как L_i=L_i(t), центр - как c_i=c_i (t), а значение приписанной ему накопленной функции d -как w_i = w_i(t).

В данной работе в качестве погрешности обучения и погрешности прогнозирования считается среднеквадратическое отклонение:

где: M – объем выборки,  – полученное значение, d – эталонное значение.

Для решения поставленной задачи была разработана программа, производящая прогнозирование с помощью нейронной сети Ванга-Менделя. В качестве прогнозируемого значения были использованы курсы акций компании Yahoo [2]. Стоимость акций в долларах взята в период с 20.04.2016 по 16.04.2017.

Также проведены исследования зависимости погрешностей обучения и прогнозирования от разных параметров:

·     Эффективности алгоритма обучения от значения предельного евклидового расстояния между входным вектором и центром кластера;

·     Погрешности обучения от объема обучающей выборки;

·     Погрешности прогнозирования от способа разделения исходных данных на две выборки: обучающую и тестирующую;

·     Погрешности прогнозирования от размера скользящего окна.

1.  Эффективность алгоритма обучения – предельное эвклидово расстояния между входным вектором и центром кластера.

Для исследования использована обучающая выборка объемом 240 наблюдений, размер плавающего окна – 2. Как видно на рисунке 2, где изображена зависимость погрешности обучения от значения предельного эвклидова расстояния между входным вектором и центром кластера, с увеличением евклидова расстояния также увеличивается значение погрешности обучения.

Рисунок 2. Зависимость погрешности обучения от значения предельного эвклидова расстояния между входным вектором и центром кластера

2.  Погрешность обучения – объём обучающей выборки.

Для исследования установлен размер плавающего окна, равный 5. На рисунке 3 изображена зависимость погрешности обучения от объёма обучающей выборки. По графику видно, что в целом погрешность уменьшается. Повышение значения погрешности (при объеме равном 200) может быть обусловлено резким колебанием курса акций.

Рисунок 3. Зависимость погрешности обучения от объёма обучающей выборки

3.  Погрешность прогнозирования – способ разделения исходных данных на две выборки: обучающую и тестирующую.

Для данного исследования размеры обучающей и тестирующей выборок варьируются таким образом, чтобы в сумме объем наблюдений был равен 250.

Рисунок 4. Зависимость погрешности прогнозирования от способа разделения обучающей выборки на две части: обучающую и тестирующую

Из рисунка 4 можно сделать вывод, что в целом, увеличение обучающей выборки и уменьшение тестирующей способствует уменьшению погрешности прогнозирования.

4.  Погрешность прогнозирования – размер скользящего окна.

Для данного исследования взяты объем обучающей выборки равный 230, тестирующей – 20. Исходя из рисунка 5 (на котором изображена зависимость погрешности прогнозирования от размера скользящего окна), для выбранных данных и объемов выборок, значение погрешности прогнозирования увеличивается с увеличением размера скользящего окна.

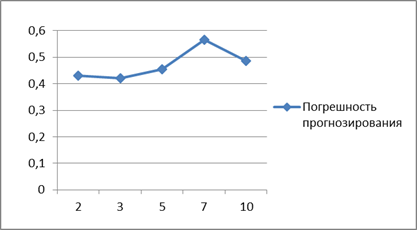
Рисунок 5. Зависимость погрешности прогнозирования от размера скользящего окна

Исходя из проведенных исследований, можно сделать вывод, что на точность прогноза влияет не только предельное эвклидово расстояние между входным вектором и центром кластера и размер обучающей выборки, но также и размер плавающего окна. Наилучшие результаты по прогнозу дают обучающая выборка размером 240, предельное евклидово расстояние равное 0,005 и размер плавающего окна, равный 3.