Эконометрическое моделирование ипотечного кредитования

Аннотация. В данной статье рассматривается влияние различных факторов на объем ипотечного жилищного кредитования в регионах Российской Федерации. Проведен регрессионный данных за 2019 год. Данные собраны из открытых источников рейтингового агентства ООО «РИА Рейтинг». Анализ проводился средствами прикладного пакета программ «Statistica».

Ключевые слова: эконометрика, моделирование, анализ, метод, регрессионный анализ, фактор, статистика, прогнозирование, объем ипотечного жилищного кредитования.

Регрессионный анализ - метод моделирования измеряемых данных и исследования их свойств. Данные состоят из пар значений зависимой переменной (переменной отклика) и независимой переменной (объясняющей переменной). Регрессионная модель есть функция независимой переменной и параметров с добавленной случайной переменной.

Цель регрессионного анализа – с помощью уравнения регрессии предсказать ожидаемое среднее значение результирующей переменной.

Рассмотрим набор данных из 15 переменных:

Y1 – Объем ипотечного жилищного кредитования в РФ, млн. руб.;

X1 – Среднедушевые денежные доходы населения, руб.;

X2 – Число браков, шт.;

X3 – Численность населения, тыс. чел.;

X4 – Ввод в действие жилых домов, тыс. кв. м.;

X5 – Численность рабочей силы, тыс. чел.;

X6 – Численность занятого населения, тыс. чел.;

X7 – Численность родившихся, млн. чел.;

X8 – Число разводов, шт.;

X9 – Величина прожиточного минимума, руб. в мес.;

X10 – ВРП на душу населения, тыс. руб.;

X11 – Среднемесячная номинальная начисленная заработная плата, руб.

X12– Средний размер назначенных пенсий, руб.;

X13 – Ставка ипотечного жилищного кредитования, %;

X14 – Ставка рефинансирования, %.

Построение регрессионной модели осуществляется при помощи программы Statistica. Необходимо построить корреляционную матрицу, описывающую зависимости между рассматриваемыми факторами, оценить эти зависимости, а также произвести регрессионный анализ вышеописанных факторов.

Проверим коллинеарность факторов, построив матрицу парных коэффициентов корреляции (Рисунок 1).

Рисунок 1. Матрица корреляций

Рассмотрев данную матрицу можно сделать вывод о том, что результативный признак (объем ипотечного жилищного кредитования в РФ, млн. руб.) имеет сильную зависимость со следующими факторами: X1, X2, X3, X4, X5, X6, X7, X8, X11.

И слабую зависимость с факторами: X9, X10, X12, X13, X14.

Связь результативного признака с факторными велика. В среднем она превышает значения матрицы межфактоных корреляций, поэтому стоит приступить к исключению менее значимых факторов.

Проведем построение регрессионной модели с учетом всех факторов, как значимых, так и незначимых. Результаты построения представлены на рисунке 2.

Регрессионная статистика показывает, что коэффициент корреляции равен 0,984, а коэффициент детерминации 0,968, что говорит о том, что модель является качественной и 97% факторов были учтены в модели.

Рисунок 2. Итоговая таблица регрессии (стандартный метод)

Величина Бета-коэффициентов позволяет сравнивать относительный вклад каждой независимой переменной в предсказание зависимой. Как видно из таблицы результатов, переменные X1 (Среднедушевые денежные доходы населения, руб.), X2 (Число браков, шт.), X3 (Численность населения, тыс. чел.), X4 (Ввод в действие жилых домов, тыс. кв. м.), X5 (Численность рабочей силы, тыс. чел.), X6 (Численность занятого населения, тыс. чел.), X7 (Численность родившихся, млн. чел.), X8 (Число разводов, шт.), X11 (Среднемесячная номинальная начисленная заработная плата, руб.) являются наиболее значимыми для объема ипотечного жилищного кредитования в РФ (значимые переменные).

С учетом всех факторов при проведении анализа данных получается следующая модель:

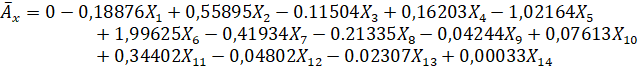
О данной модели можно сказать то, что каждый коэффициент регрессии при факторном признаке показывает на сколько единиц измениться объем ипотечного жилищного кредитования в РФ при аналогичном изменении какого-либо из исследуемых факторных признаков на 1 соответствующую единицу измерения.

Для проверки значимости данной модели необходимы два показателя Fнабл и Fкрит (F-критерий Фишера), которые определяются по таблице значений F-критерия.

Fнабл = 152,83

Fкрит = 14,70

Таким образом, Fнабл > Fкрит.

Следовательно, гипотеза о статистической значимости и надежности уравнения применяется при уровне значимости 0,05.

Чтобы исключить факторы, которые не являются значимыми, можно воспользоваться стандартным методом, методом исключения и методом включения факторов.

При использовании стандартного метода получилось 8 значимых факторов, представленных на рисунке 2.

Воспользуемся методом исключения (рисунок 3).

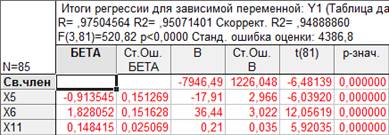
Рисунок 3. Итоговая таблица регрессии (метод с исключением)

Данный метод позволил сделать вывод, что значимыми являются 3 фактора: X5, X6, X11.

Так как метод исключения зачастую убирает излишнее количество факторов, рациональнее использовать метод включения. Проведем включение значимых факторов в модель и получим следующее (рисунок 4):

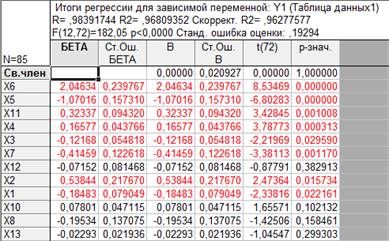
Рисунок 4. Итоговая таблица регрессии (метод с включением)

Чтобы получить только значимые факторы необходимо исключить все незначимые факторы.

После постепенного исключения всех незначимых факторов получим следующее (рисунок 5):

Рисунок 5. Итоговая таблица регрессии (метод с включением)

По таблице на рисунке 5 видно, что значимыми являются 5 факторов: X4 – Ввод в действие жилых домов, тыс. кв. м.; X5 – Численность рабочей силы, тыс. чел.; X6 – Численность занятого населения, тыс. чел.; X7 – Численность родившихся, млн. чел.; X11 – Среднемесячная номинальная начисленная заработная плата, руб.

По регрессионной статистике можно сделать вывод о том, что модель является качественной, так как коэффициент детерминации близок к единице (R2 = 0,95) и значительно превышает критическую отметку 0,8. Наблюдаемое значение F велико (Fнабл = 351,20) и превышает F критическое, следовательно, можно сделать вывод о том, что гипотеза о статистической значимости и надежности уравнения принимается при уровне значимости 0,05. Показатель множественной корреляции, равный 0,978 превышает отметку 0,8 и близок к единице, т.е. связь объема ипотечного жилищного кредитования в РФ с совокупность факторов очень сильная.

Уравнение регрессии имеет следующий вид:

Интерпретируем данную модель:

При увеличении объема ввода в действие жилых домов на 1 тыс. кв. м., объем ипотечного жилищного кредитования в РФ увеличится на 0,12980 млн. руб.

При увеличении численности рабочей силы на 1 тыс. чел., объем ипотечного жилищного кредитования в РФ уменьшится на 1,08831 млн. руб.

При увеличении объема численности занятого населения на 1 тыс. чел., объем ипотечного жилищного кредитования в РФ увеличится на 2,13512 млн. руб.

При увеличении численности родившихся на 1 млн. чел., объем ипотечного жилищного кредитования в РФ уменьшится на 0,23746 млн. руб.

При увеличении объема среднемесячной номинальной начисленной заработной платы на 1 руб., объем ипотечного жилищного кредитования в РФ увеличится на 0,14575 млн. руб.

По данной модели можно сделать вывод о том, что наибольшее влияние на значение объема ипотечного жилищного кредитования в РФ оказывает объем численности занятого населения.

Проведем оценку адекватности модели. Анализ адекватности основывается на анализе остатков.

Критерием адекватности модели можно считать нормальность остатков. То есть гистограмма распределения остатков должна быть близка к графику нормального распределения. Рассмотрим нормальный вероятностный график остатков (Рисунок 6) и распределение остатков (ожидаемое нормальное) (Рисунок 7).

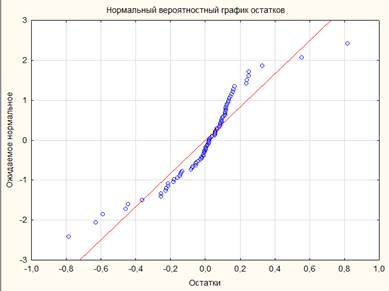
Рисунок 6. Нормальный вероятностный график остатков

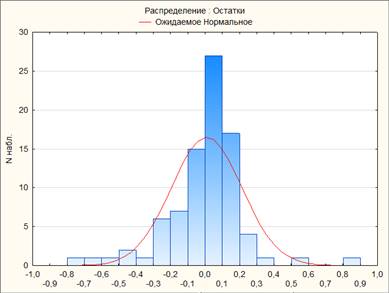
Рисунок 7. Распределение остатков

Исходя из этих графиков можно сделать вывод, что остатки образуют прямую зависимость и подчиняются нормальному закону распределения.

Таким образом можно сделать вывод, что регрессионный анализ может обеспечить понимание соотношений между различными факторами и наблюдаемым откликом. Такое понимание может помочь в принятии решений, связанных с изучаемым процессом, и будет способствовать улучшению процесса.

Регрессионный анализ позволяет оценить относительные величины влияния независимых переменных, а также относительный вклад этих переменных. Эта информация очень важна при управлении или улучшении выходных характеристик процесса.