Аффинные преобразования плоскости и их приложения к применению задач

Аннотация. Актуальность данной темы статьи заключается в углублении знаний по теме «аффинные преобразования плоскости», которое позволяет решать задачи на преобразование и их свойства. Изучаются понятия аффинных преобразований плоскости , их свойств , особенностей и применению их на практике. Целью данной работы являются рассмотрение и изучение аффинных преобразований плоскости. При раскрытии темы применяются методы : теоретический и практический. В теоретической части рассматриваются теория аффинного преобразования , изучаются свойства(групповые свойства). В практической части представлены задачи аффинных преобразований , в которой используются их групповые свойства.

Ключевые слова. аффинные преобразования, групповые свойства аффинных преобразований, теория аффинного преобразования.

Изначально отметим о том, что в случае, когда в задаче затронуты лишь такой вид свойств фигур, сохраняющиеся в процессе произвольного аффинного преобразования, такой вид задачи называют как аффинная.

В случае, когда в задаче вопрос затрагивает свойства, которые сохраняются в процессе преобразования подобия, нарушающиеся при том или ином аффинном преобразовании, такой вид задачи называют как метрическая.

К примеру, в задаче «по доказательству того, что медианы треугольника пересечены в одной точке» - является аффинной, а такой вид задач в отношении высоты и биссектрисы - метрической [3, с. 104].

Отметим, что в случае отображения плоскости P в плоскость R - закон или правило, по которому каждой точке плоскости P сопоставляется некая выявленная точка на плоскости R. Обозначают как f: P→R.

В случае, когда необходимо указать то, что точке А в плоскости Р соответственно определяется точка В на плоскости R, получаем B=f(A), в данном примере В является образом точки А, а точка А - прообразом точки В.

Совсем является не обязательным то, чтобы в каждой точке плоскости R есть определение еще какой-то точки. В случае, когда в отношении некоторого отображения плоскости P и R являются совпадающими, то данный вид отображения называют как преобразование плоскости.

Отображение f: P→R называют как взаимно однозначные, в случае, если в отношении каждой точки плоскости R имеется прообраз, и потом лишь один [5, с. 48].

В случае выбранных систем координат на плоскостях P и R отображение сопоставляется в отношении пары чисел (x, y) и пары чисел (x', y'). В свою очередь, при задаче отображения при выбранном СК - это то же самое, что и задавать два вида функций.

В этом случае, у каждой имеется зависимость от двух независимых переменных в виде: x΄=φ(x, y), y΄=ψ(x,y).

Процесс преобразования f плоскости Р называют линейным, когда на Р есть такой вид декартовой системы координат, в которой f можно записать через формулы как: x΄=a₁x+b₁y+c₁, y΄=a₂x+b₂y+c₂. Так, становится более ясно то, что взаимно однозначное линейное преобразование -аффинное.

С целью преобразования, которое задано через формулы x΄=a₁x+b₁y+c₁, y΄=a₂x+b₂y+c₂, чтобы оно являлось взаимно однозначным, нужно и достаточно, лишь:  . Так, аффинное преобразование определено через формулы: x΄=a₁x+b₁y+c₁, y΄=a₂x+b₂y+c_2 с учетом условия, что  .

Геометрическими свойствами аффинных преобразований являются такие как: к примеру, рассмотрим на плоскости прямую с уравнением  и найдем её образ при преобразовании f. (Образ прямой является множеством образов в её точках). Радиус-вектор образа М' произвольной точки М возможно определить посредством [1, с. 94]:

=                                                                                             (1),

 - постоянного вектора 

а  - радиуса-вектора точки М.

Исходя из свойств линейных преобразований получим:

.

Так как f является аффинным преобразованием, и  то перейдет в вектор  и уравнение  - это уравнение прямой линии. Таким образом, образы всех точек по прямой лежат на прямой. F определяется как взаимно однозначный вид отображения одной прямой в отношении другой [4, с. 73].

1.В случае аффинного преобразования прямая линия уходит в прямую линию, отрезок уходит в отрезок, параллельные прямые уходят в параллельные.

2.В случае аффинного преобразования отношение длин параллельных отрезков не изменен.

В доказательство приведем пример: пусть отрезки АВ и CD являются параллельными. Это выявляет то, что есть такое число λ, и образы векторов  и  связанные с зависимостью  . Ясно, что  [6, с. 28].

Получаем следующий вид следствия: в случае, если точка С разделяет отрезок АB в отношении λ, то её образ C' разделяет образ A'B' отрезка АВ в том же отношении λ.

Таким образом, выделим следующий вид свойств в аффинном преобразовании посредством:

1.Образа параллельных прямых определенные параллельными прямыми:

2. Аффинное преобразование сохраняет соотношение двух отрезков, которые расположены на одной прямой AB/CD=A΄B΄/C΄D΄:

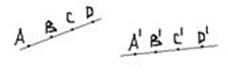
3. Аффинное преобразование сохраняет соотношение параллельных отрезков.

4. Аффинное преобразование угла и отношение произвольных отрезков не сохраняется, ведь любой треугольник возможно перевести в любой иной. Так высота и биссектриса треугольника преобразуемы обычно в иные виды линий, медиана также может переходить в медиану, а середина отрезка может переходить в середину.

Таким образом, в случае аффинного преобразования параллелограмм переходит в параллелограмм, трапеция в трапецию [2, с. 57].