Моделирование при решении задач на различные процессы в начальной школе

В начальном курсе математики одной из ключевых дидактических линий является раздел «Текстовые задачи». Обучение решению текстовых задач начинается еще в дошкольный период, когда дети знакомятся с простейшими задачами [4, с. 58], и продолжается в начальной школе. Особая роль в их освоении отводится формированию умений строить модели и схемы [1], ведь моделирование относится к метапредметным умениям, обозначенным в ФГОС НОО как познавательное универсальное учебное действие [5, с. 8].

В начальной школе дети решают простые и составные текстовые задачи, а также задачи на различные процессы, прежде всего, на работу, движение, «куплю-продажу» [3]. Основное правило, которому подчиняется решение любой текстовой задачи: по двум известным величинам найти третью; при этом особенно важно определить зависимость между ними.

Установим далее, в каких отношениях находятся величины, описывающие различные процессы и основные виды моделей, рассматриваемые в начальной школе при изучении текстовых задач на процессы. 

Работа характеризуется тремя величинами: производительностью труда (W), временем (t), объемом всей работы (A). Основная формула, связывающая отношения между ними, имеет вид A = W × t. Отсюда нетрудно составить правила для нахождения производительности труда и времени, затраченного на работу:

W = A : t и t = A : W.

Для запоминания формул мы предлагаем использовать на уроке вспомогательную схему – треугольник (рис. 1). В верхнюю его часть («на верхний этаж») поместим величину А, которая находится путем умножения величин, находящихся на «нижнем этаже»: W и t. В свою очередь, чтобы найти производительность труда или время, находящиеся на «нижнем этаже», нужно выполнить операцию деления.

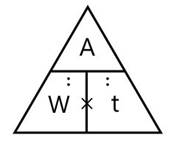
Рисунок 1. Вспомогательный треугольник в задачах на работу

В начальном курсе математики широко используются знаковые модели – таблицы, как, например, табл. 1.

Таблица 1.

Вспомогательная модель в задачах на работу

Задачи на «куплю-продажу» относят к задачам на процессы, так как величины: цена (a), количество (n) и общая стоимость (C) покупки также подчиняются рассмотренному правилу: одна величина находится путем умножения двух других, а, значит, две оставшиеся величины находятся путем деления. Вспомогательный треугольник составляем по тому же принципу, что и в задачах на работу (рис. 2).

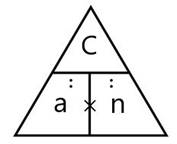
Рисунок 2. Вспомогательный треугольник в задачах на «куплю-продажу»

Вспомогательная таблица при этом имеет следующий вид:

Таблица 2.

Вспомогательная модель в задачах на «куплю-продажу»

В начальном курсе математики рассматриваются задачи на расход материала, принцип решения которых полностью соответствует алгоритму решению задач на работу и «куплю-продажу». Основными величинами, характеризующими этот процесс, являются: расход на одно изделие, количество изделий, общий расход (табл. 3).

Таблица 3.

Вспомогательная модель в задачах на расход материалов

Отметим, что основным процессом, рассматриваемым в начальной школе, является движение, характеризующееся пройденным расстоянием (S), скоростью движения (V) и временем движения (t):  S = V × t. Вспомогательный треугольник при этом имеет вид как на рис. 3, а табличная модель представлена в виде табл. 4.

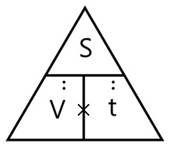
Рисунок 3. Вспомогательный треугольник в задачах на движение

Таблица 4.

Вспомогательная модель в задачах на движение

Таким образом, с помощью таблиц и вспомогательных треугольников, мы можем заметить взаимосвязь величин, характеризующих различные процессы. Например, стоимость соответствует расстоянию, общему расходу материалов, работе, цена – скорости, производительности труда, а количество единиц товара – времени. Осознание общности изучаемых процессов может привести школьников к пониманию, что все они описываются одной формулой:

a = b × с,

откуда, зная произведение и один из множителей, без труда находим неизвестный множитель. Таким образом, решение задач на процессы в начальной школе является пропедевтикой изучения функциональной линии в основной школе [2].

Задачи на движение широко представлены в курсе математики начальной школы. Среди них можно выделить следующие типы задач:

- задачи на встречное движение. В этом случае рассматривается скорость сближения, определяемая как сумма скоростей сближающихся объектов:

V_сбл. = V₁ + V₂;

- задачи на движение в противоположных направлениях из одного пункта. Здесь рассматривается скорость удаления: V_удал. = V₁ + V₂;

- задачи на движение в одном направлении (с отставанием и вдогонку), тоже характеризующееся скоростью удаления: V_удал. = V₁ – V₂, где V₁ > V₂.

- задачи на движение в прямом и обратном направлении: из пункта А в пункт B, а затем обратно;

- задачи на движение с остановками.

Приведем пример задачи на встречное движение: Белоснежка и Золушка решили встретиться около замка, и вышли навстречу друг другу. Они встретились через 2 часа. Белоснежка шла со скоростью 4 км/ч, а Золушка – 3 км/ч. На каком расстоянии они находились изначально друг от друга?

Для решения  этой задачи можно составить вспомогательную модель (рис. 4), табличную модель (табл. 5) и решающие арифметические модели (первый и второй способ решения).

Рисунок 4. Вспомогательный рисунок в задаче на встречное движение

Таблица 5.

Вспомогательная табличная модель в задаче на движение

Первый способ. Зная, что сказочные персонажи встретились через два часа, мы можем узнать расстояние между двумя пунктами. Найдем расстояние, которое прошли герои сказок за 2 часа по отдельности.

1) 4 × 2 = 8 (км) – прошла Белоснежка;

2) 3 × 2 = 6 (км) – прошла Золушка;

3) 8 + 6 = 14 (км) – было расстояние между Белоснежкой и Золушкой.

Второй способ. Белоснежка за один час преодолевала 4 км, а Золушка – 3 км, значит, обе за один час преодолевали 4 + 3 = 7 км, тогда за два часа они преодолели 7 × 2 = 14 км. Запишем решение по действиям:

1) 4 + 3 = 7 км/ч – скорость сближения;

2) 7 × 2 = 14 км – было расстояние между Белоснежкой и Золушкой.

Ответ: 14 км.

Решение задачи различными способами не только развивает вариативность мышления учащихся, но и является проверкой адекватности составленной школьниками арифметической модели задачи. Таким образом, при изучении темы «Текстовые задачи» школьники усваивают как предметные, так и метапредметные умения, в частности, учатся моделировать, схематизировать и выполнять проверку адекватности составленных моделей.