Виды задач с элементами историзма на уроках алгебры

Главным средством для развития у школьников сильной заинтересованности к предмету математики, к ее истории – это постановка перед учащимися проблемных задач, а именно, задач историко-математического содержания. Эти задачи реализуют следующие функции: вводно-мотивационную, иллюстративную и конкретизирующую, контрольно-оценочную, способствуют развитию творческого мышления и воображения.

Под старинными задачами понимают задачи из исторических математических источников, начиная с древнеегипетских математических папирусов и заканчивая сборниками отечественных старинных задач.

В работах Ю. М. Колягина, Е. И. Лященко, Г. И. Саранцева и др. изучался вопрос о функциях задач в обучении математике. Наиболее полная их характеристика приведена в работах Ю. М. Колягина:

• под образовательными функциями задач в обучении математике подразумевают такие функции, которые направлены на формирование у учеников системы математических знаний, умений, навыков, как предусмотренных программой, так расширяющих и углубляющих ее содержание;
• под воспитательными функциями подразумевают функции, которые формируют не только познавательный интерес учащихся, но и их самостоятельность, навыки учебного труда, а также нравственные качества;
• к развивающим функциям задач относятся функции направленные на развитие мышления учащихся, на овладение ими эффективными приемами деятельности.

Д. В. Смоляковой разработаны типы учебных заданий с элементами истории математики, способствующих:

• обогащению различных форм кодирования информации;
• учету закономерностей формирования понятийного опыта учащихся;
• обогащению метакогнитивного опыта учащихся;
• обогащению эмоционально-оценочного опыта учащихся [5, с. 22].

О. Н. Журавлевой установлено, что при обучении математике задачи, содержащие в себе элементы ее истории эффективны в следующих направлениях: прежде всего - это выявление методологических, а затем общекультурных, гуманитарных компонентов математического знания [1, с. 60]. Осуществление первого направления при включении таких задач в процесс обучения является важной в связи с актуальными концепциями фундаментализации образования и деятельностного подхода. Для учеников создается возможность получить представление о способе (средстве, идее) решения, который отличается от предложенного в школьных учебниках, знакомство с разнообразными формулировками предположений, рассуждений и доказательств в математике, а также сопоставление различных методов решения задач математики. Все приобретенные знания и умения ученики в дальнейшем смогут использовать для того, чтобы найти выход из других возникающих у них проблем. Не менее значимым для более глубокого понимания сущности рассматриваемых математических объектов может быть реализовано и второе направление с помощью использования задач историко-математического содержания: основные линии взаимосвязи науки математики и культуры, непохожие стороны и направления приложения математики в гуманитарной сфере. Использование и изучение задач историко-математического содержания сможет помочь приобщить учеников к общечеловеческим ценностям и всем областям деятельности людей (практико-ориентированной, научной и т. д.), позволяет углубить знания по предмету.

На основе всего вышесказанного выделим виды задач в зависимости от выполняемых ими функций.

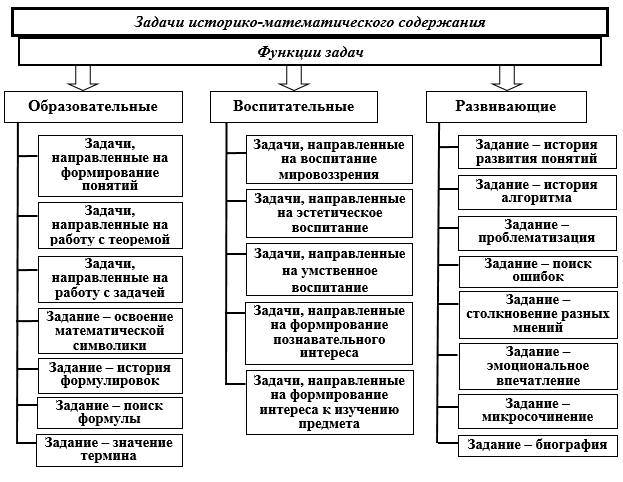
Рисунок 1. Виды задач в соответствии с их функциями

Такие задачи можно с легкостью интегрировать с содержанием уроков алгебры любого типа. Приведем примеры таких задач при изучении темы «Сумма n первых членов геометрической прогрессии».

На этапе применения понятия, для реализации образовательной функции, можно предложить учащимся задачу Архимеда [3, с. 24]:

Найти сумму бесконечно убывающей геометрической прогрессии

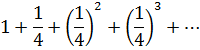
После решения с учащимися данной задачи можно привести им в современной символике решение Архимеда, которое он дал в трактате «О квадратуре параболы».

Для реализации воспитательной функции учащимся можно предложить задачу, направленную на формирование познавательного интереса и интереса к изучаемому предмету из «Арифметики» Л. Ф. Магницкого в современной формулировке:

Некий человек продавал коня за 156 рублей. Купец, покупая, подумал, что конь не достоин такой высокой цены. Тогда продавец предложил ему иную «куплю». «Если тебе кажется, что цена этому коню велика, купи только гвозди для подков, а коня же возьми даром. Гвоздей в каждой подкове по шесть, и за один гвоздь дашь мне одну полушку, за другой – две полушки, а за третий копейку и так все гвозди купи». Купец же, видя столь малую цену и желая получить коня даром, обещал выплатить эту цену, думая заплатить не более 10 рублей за гвозди. Проторговался ли он [6. с. 42]?

При решении на уроке данной задачи учащиеся вспомнят арифметические способы решения задач. В тексте встречается устаревшее слово – «полушка» (серебряный монетный номинал – четверть копейки), так ученики могут получить знания о цене товаров того времени. Им будет интересно узнать, что в подкове коня 6 гвоздей, а также, что купец делает покупку не для себя, а для последующей продажи, с целью получения прибыли.

Для реализации развивающей функции при изучении данной темы учащимся можно предложить задание – поиск ошибок, т. е. привести известный софизм Зенона из города Элеи:

«Чтобы пройти путь в один километр, нужно непременно миновать его середину», утверждал Зенон. «Если мы дошли до середины пути, перед нами остаётся ещё полпути, у которого есть своя середина. И так без конца. Сколько бы мы не шли, впереди всегда есть какая-то не пройденная часть пути, у которой есть своя середина» [3, с. 37].

Разбор математических софизмов позволяет развить у учащихся умение находить ошибки, указывать их причины, прогнозировать возможные ошибки. Исследование ошибок, которые известны в истории математики, может помочь ученикам быть чувствительными к проблемам, видеть «болевые точки», знание которых является профилактикой ошибочных действий.

В заключение статьи отметим, что на большинстве уроков алгебры задачи с элементами историзма могут выполнять те функции, которые выполняет учебный материал. Эффективное включение таких задач в содержание уроков будет способствовать и формированию познавательных интересов учащихся, и более глубокому пониманию изучаемого материала, и расширению кругозора учащихся, и решению других многочисленных задач, возникающих в практике обучения.