Построение таблиц истинности логических функций с использованием СКА Maple

Курс школьной информатики затрагивает большое количество тем, одной из которых является алгебра логики [5]. Логика одна из древнейших наук. Первые идеи логики, были изложены древнегреческим философом Аристотелем в своей работе «Органон». В связи с этим именно его считают основателем данной науки. Он привел в систему формы и правила мышления, провел исследования, результатом которых стала теория умозаключений и доказательств. Кроме того, он описал ряд логических операций, сформулировал основные законы формальной логики.

В конце XIX – начале XX в.в. в логике возникло новое направление, которое получило название – математическая логика. В последствие эта теория получила название классической логики.

В свою очередь, математическую логику делят на два основных раздела: логика высказываний и логика предикатов.

Алгебра логики (логика высказываний) – это один из основных разделов математической логики. В этом разделе методы алгебры используются для преобразования логических высказываний.

Высказывание - это термин математической логики, которым обозначается предложение какого-либо языка (естественного или искусственного), рассматриваемого лишь в связи с его истинностью. Например: «Луна – спутник Земли» – Истина; «10>3+8» – Ложь; «Россию омывают 13 морей» – Истина; «Тигр – домашнее животное» – Ложь [3; 4].

Но не все высказывания являются логическими. Так, например, предложения «На улице ветрено», «Как настроение?», «3х-1>10» не будут относиться к логическим высказываниям.

Для понимания и наглядного представления значений логической функции в рамках школьной информатики рассматривается построение таблиц истинности.

Таблица истинности – это таблица, в которой отражены все значения логической функции при всех возможных значениях, входящих в неё логически.

В данном случае «логическая функция» это функция, у которой значения переменных (параметров функции) и значение самой функции выражают логическую истинность. Например, в двузначной логике они могут принимать значения «истина» либо «ложь» (truе либо fаlse, 1 либо 0) [4].

Для построения таблицы истинности необходимо соблюдать определенную последовательность действий:

1)  Подсчитать количество логических переменных n.

2)  Подсчитать количество строк .

3)  Количество столбцов = n+ количество логических операций.

Рассмотрим таблицы истинности для основных логических операций. Для их построения можно использовать систему компьютерной алгебры Maple, в котором имеется специализированный пакет команд Logic, разработанный для решения типовых задач двузначной булевой логики [1].

1.  Логическое умножение или конъюнкция.

Составное высказывание A&B истинное тогда, когда А истинно И В истинно (Рис.1).

Рисунок 1. Таблица истинности для конъюнкции: а) общепринятое представление б) представление в СКА Maple 16 с использованием команды TrueTable

2.  Логическое сложение или дизъюнкция.

Составное высказывание (А В) истинное, когда А ИЛИ В истинны (Рис. 2).

Рисунок 2. Таблица истинности для дизъюнкции: а) общепринятое представление б) представление в СКА Maple 16 с использованием команды TrueTable

3.  Логическое отрицание или инверсия.

Если выказывание «А истинно» =A, то «НЕ A – ложно» =А (Рис. 3).

Рисунок 3. Таблица истинности для инверсии: а) общепринятое представление б) представление в СКА Maple 16 с использованием команды TrueTable

4.  Логическое следование или импликация.

ЕСЛИ А истинно, ТО B истинно (Рис. 4).

Рисунок 4. Таблица истинности для импликации: а) общепринятое представление б) представление в СКА Maple 16 с использованием команды TrueTable

5.  Логическая равнозначность или эквивалентность.

Высказывание А ~ B истинно тогда, когда А И В истинны ИЛИ А И В ложны (Рис. 5).

Рисунок 5. Таблица истинности для эквивалентности: а) общепринятое представление б) представление в СКА Maple 16 с использованием команды TrueTable

Рассмотрим порядок построения и проверки правильности функционирования таблиц истинности в СКА Maple на примере решения задачи [2; 3].

Построить таблицу истинности для следующего выражения: A&BC

1.  Подключим необходимую библиотеку:

> with(Logic)

2.  Введем данное выражение:

> F:=A &and B &implies C

3.  Построим таблицу истинности для данного выражения:

> T1:= TruthTable(F)

Использование СКА Maple организуется путем создания и использования в среде этой системы педагогических программных средств – так называемых Maplet, предоставляющих возможность воспроизводить пошаговое решение типовых задач высшей математики [5].

Проиллюстрируем такой подход примером решения представленной выше задачи.

Maplets «Таблицы истинности»: 

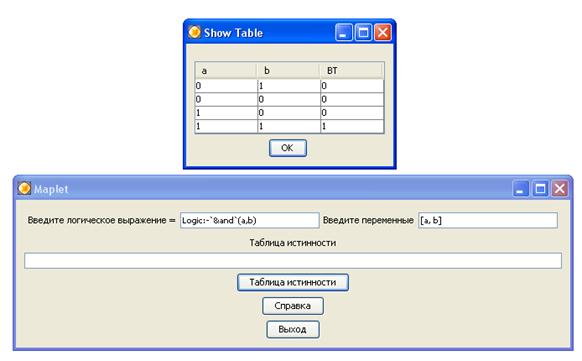
> restart;with(Logic):

F:=proc () local x,y,BT,L,res,ind,ent:

> BT:=Maplets [Tools][Get]('Tx'::function):

L:=Maplets [Tools][Get]('Ty'::list):

> res:=TruthTable(BT,L, form=MOD2);

ind:=indices(res);

ent:=entries(res);

Maplets[Examples][ShowTable]([[op(L),"BT"],seq([op(ind[i]),op(ent[i])],i=1..2^nops(L))]);

> end proc: #F

> with (Maplets[Elements]):

fn:=font=Font(10):

c1:="Введите логическое выражение =",TextField['Tx'](fn,'value'=&and(a,b)):

c2:="Введите переменные",TextField['Ty'](fn,'value'=[a,b]):

mx:="Таблица истинности",TextBox['T1'](fn,width=4):

bmx:=Button(fn2,"Таблица истинности",Evaluate('T1'="F()")):

bmxy:=Button("Справка", Evaluate(function = "Maplets[Display](maplet2)")):

my:=Button("Выход", Shutdown(['Tx'])):

> maplet2 := Maplet(

 MessageDialog("Логическое выражение вводить с учётом правил библиотеки Logic, переменные участвующие в построениии таблицы истинности,вводить в квадратных скобках через запЯтую")

):

> mplt:=Maplet (Window([ [c1,c2],mx, bmx,bmxy,my])):

Maplets [Display](mplt):

Таким образом, maplets «Таблица истинности» позволит быстро построить таблицу истинности для введенного логического выражения, и выполнять проверку правильности полученных результатов [6].