Элементы математической логики в начальном курсе математики

В современной системе обучения в условиях реализации федерального государственного образовательного стандарта начального общего образования последнего поколения наметился перенос акцентов с увеличения объема информации для усвоения учащимися на формирование у школьников общелогических мыслительных умений: анализ, синтез, абстрагирование, классификация, сравнение, сериация, подведение под понятие и т.д., так как интеллект человека определяется не суммой накопленных им знаний, а высоким уровнем логического мышления и умением применять полученные знания в нестандартных ситуациях. Формирование и развитие основных логических структур мышления, по мнению психологов, происходит в возрасте от 4 до 10 лет, то есть в период обучения ребенка в начальной школе.

Появление в последние годы в учебно-методической литературе специальных разработок по обучению решению логических задач и развитию логического мышления младших школьников говорит о том, что рассматриваемая проблема приобретает особую актуальность [2]. О необходимости и возможности обучения элементам математической логики в начальной школе свидетельствуют также разнообразные дидактические материалы для разновозрастных групп учащихся начальной школы, включение логических задач в задания контрольных и проверочных работ, олимпиад разного уровня.

В работах отечественных ученых А.М. Пышкало, Н.Я. Виленкина, А.А. Столяра, Н.Г. Салминаой, А.П. Тонких, Н.И. Стяжкина и др. освещены принципиальные вопросы совершенствования школьного математического образования, в частности, вопросы, связанные с усилением логической основы школьного курса, включением в него элементов математической логики [1].

Проблема введения элементов логики при обучении математике состоит не в том, чтобы специально и обособленно изучать логику, как отдельный учебный предмет или отдельную дидактическую линию, а в том, чтобы необходимые элементы логики стали неотъемлемой частью самого преподавания математики, важным инструментом, повышающим его эффективность и влияние на логическое развитие учащихся. По мнению А.А. Столяра, «необходима мыслительная, логическая программа, которая должна быть реализована в начальных и средних классах школы» [5, с. 17].

Рассмотрим, какое место занимают элементы логики в содержании современных курсов начальной математики. Некоторые образовательные программы начального курса математики вводят в ознакомительном плане элементы формальной логики и теоретико-множественные операции, но не применяют их в дальнейшем для построения выводов, умозаключений.

В программе Н.Г. Салминой, В.А. Тарасовой в число предварительных умений, необходимых для усвоения математических знаний, включены некоторые логические операции, знаково-символические умения и простейшие математические отношения и зависимости. Введение этих знаний в начало обучения до знакомства с числом дает возможность не только сделать доступными важнейшие математические понятия и действия, но и повысить научный уровень усвоения знаний. В русле данной программы типичными являются задания, где необходимо выявить и использовать логические взаимосвязи, например, как в следующем задании.

Задание 1. Продолжите последовательность:

1) 2, 3, 5, 6,8, 9, __, __.

2) 10, 5, 9, 4, 7, __, __.

3) 4, 6, 7, 9, 10, 12, __, __.

В книге «Информатика в играх и задачах» А.В. Горячева [3] рассматриваются правила составления описаний предметов (объектов), их поведения и логических рассуждений о них в виде требований к строгости и логической аккуратности составления таких описаний. Для проверки правильности различных суждений и их комбинаций можно использовать метод, широко используемый в теории множеств, согласно которому множества и отношения между ними можно изображать в виде геометрических фигур. Таким образом, логические рассуждения проводятся с помощью наглядности, что также способствует развитию наглядно-образного мышления младших школьников.

Задача 2. Пусть А – множество людей, умеющих плавать; В – множество людей, умеющих играть на скрипке. Что представляет собой обведенная область (рис. 1)? Ответ: люди, умеющие плавать и играть на скрипке.

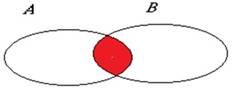
Рисунок 1. Иллюстрация к задаче 1

Описанный метод геометрической иллюстрации логических рассуждений был предложен великим математиком XVIII в., петербургским академиком Леонардом Эйлером и широко применялся английским математиком Джоном Венном. Поэтому такие рисунки называются диаграммами Эйлера-Венна.

Приведенные задания могут быть использованы не только на уроках информатики, но и на уроках математики в начальной школе, ведь «Информатика» как учебный предмет реализуется в начальной школе только за счет регионального компонента, а, значит, не во всех школах. В тоже время в федеральном государственном образовательном стандарте начального общего образования раздел «Информатика» вводится как составная часть предметной области «Математика и информатика», а, значит, на учителя начальной школы накладывается дополнительная ответственность по обучению элементам математической логики. 

В разработанном Л.Г. Петерсон непрерывном курсе математики «Учусь Учиться» на ранних стадиях обучения, опираясь на житейский опыт учащихся и конкретные примеры, вводятся понятия множества как «группа предметов, совокупность», отношения между ними, графические диаграммы Венна, понятия «верные и неверные высказывания». Одной из целей данного курса является применение формальной логики, построение выводов путем применения к известным утверждениям логических операций «если... , то... », «и», «или», «не». Также в этой программе приводятся задания на установление закономерностей, как, например, в следующем задании.

Задание 3. Дан ряд фигур (рис. 2).

Рисунок 2. Ряд фигур

Необходимо выявить закономерность и подобрать из предложенных фигур пару к данным (рис. 3).

Рисунок 3. Фигуры для продолжения ряда

В соответствии с программой по математике В.Н. Рудницкой учебно-методического комплекса «Начальная школа XXI века», учащиеся овладевают многими важными логико-математическими понятиями. Они знакомятся с математическими высказываниями, логическими связками («и», «или», «если, то», «неверно, что»), со смыслом логических слов (каждый, любой, все, кроме), составляющими основу логической формы предложения, используемой в логических выводах. Важной составляющей линией логического развития ребенка является его обучение (уже с I класса) действию классификации по заданным основаниям и проверка правильности его выполнения [3, с. 27].

Обучение по предложенной программе способствует не только расширению математических знаний в области формальной логики, но и повышению качества знаний четвероклассников. Использование элементов математической логики при выполнении заданий повышает уровень культуры интеллектуального труда учащихся, развивает логическое мышление, математическую память, внимание, сообразительность и смекалку детей.

Таким образом, мы выявили, что различные программы по математике содержат ряд заданий, способствующие как развитию логического мышления младших школьников, так и усвоению ими элементов математической логики на последующих этапах обучения.