Комбинаторные задачи как средство формирования познавательных УУД младших школьников на уроках математики

Перед современными российскими школами одной из главных задач является воспитание детей, как личности. Умеющих анализировать факты, самостоятельно, разумно мыслить и находить выход из различных ситуаций, выбирая наилучший путь из существующих. В соответствии с этим, все общеобразовательные школы в России ориентированы на то, чтобы образование давало нашим обучающимся не только получение определенных знаний, но и познавательные и созидательные возможности. Поэтому педагоги были вынуждены внести коррективы в методику преподавания начального курса математики [3]. И важнейшей задачей, которая стояла перед педагогами, стала формирование универсальных учебных действий, которые входят в состав метапредметных результатов обучения.

В соответствии с принятой классификацией выделяют личностные, регулятивные и познавательные УУД. В свою очередь, познавательные УУД включают в себя общеучебные и логические учебные действия, постановка и решение проблемы. К общеучебным УУД относят: формулирование познавательной цели, поиск и выделение информации, знаково-символические действия, моделирование. К логическим УУД относят: действие анализа; построение логической цепи рассуждений; действие синтеза; действие сравнения; действие классификации; подведение под понятие или отнесение к известным понятиям; выдвижение гипотез и их обоснование; доказательство предположений, гипотез и т.д. Постановка и решение проблемы включает в себя формулирование проблемы; самостоятельное создание способов решения проблем творческого и поискового характера.

Данными действиями в начальном курсе математике можно овладеть при помощи решения комбинаторных задач. Вспомним, что комбинаторными задачами, называются такие задачи, где ответ находится путем выбора из всех предложенных комбинаций объектов [2].

Можно заметить, что комбинаторные задачи рассматриваются ещё в дошкольном возрасте. Изучая данные задачи целенаправленно,они способствуют развитию вариативности мышления, т.е. мыслительной деятельности ученика, которая способна находить различные решения задачи в случае, когда нет специальных указаний на это.

На основе анализа учебно-методических комплексов по математике начальной школы можно выявить следующую типологию комбинаторных задач, используемых в начальном курсе математики:

1) Задачи, которые решаются методом графа;

Пример: Из города А в город В ведут пять дорог, а из города B в город С — три дороги. Сколько путей, проходящих через В, ведут из А в С?

Данная задача направлена на пропедевтику. Решение её будет выглядеть следующим образом:

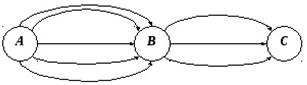
Рисунок 1. Граф

1) Перестановки;

Пример. У Кати на обед – первое, второе, третье блюда и конфета. Она начнёт свой обед именно с торта, а всё остальное будет кушать в произвольном порядке. В какой последовательности она может съесть блюда?

Данную задачу  можно решить методом упорядоченного перебора или с помощью «дерева вариантов», которое является одним из разновидностей графа. Но в отличии от графа, дерево решений характеризуется тем, что «растёт сверху вниз».Данный вид удобен для расположения объектов в нужной последовательности [2].Решение будет выглядеть следующим образом: Обозначим первое блюдо – П, второе блюдо – В, третье блюдо – Т, конфета – К.

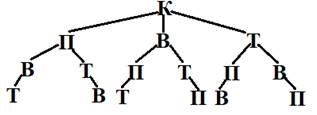
Рисунок 2. Дерево решений

Ответ: 6.

2) Сочетания без повторения;

Сколько разных букетов можно создать из двух цветов, если в вашем распоряжении 3 цвета: ромашка, лилия, тюльпан (цветы в букете не должны повторяться)?

Данную задачу можно решить с помощью таблицы. В данном случае получилось, что заполнены только три колонки, диагональные не заполнены потому что они соответствуют цветам, состоящих из одинаковых цветов, а остальные потому, что ТЛ и ЛП составляет один и тот же букет, поэтому данные варианты не учитываются.

Таблица 1.

Варианты создания букетов

Пример: Сколько двухзначных чисел можно составить из цифр 2, 5, 7 (цифры в записи числа не должны повторяться)?

Данную задачу можно решить при помощи таблицы. В данном случае будет играть порядок выбора цифр, ведь число 25 и 52 – разные числа, поэтому почти все колонки оказались заполненными, кроме диагональных, которые соответствуют числам, состоящих из одинаковых цифр.

Таблица 2.

Варианты составления двухзначных чисел

4) Комбинаторные задачи с геометрическим содержанием. Данные задачи являются незаменимым средством развития геометрических представлений обучающихся. В процессе решений данных задач совершенствуется наглядно-образное, наглядно-действенное и абстрактное мышление [3].

Пример: Разложи на полке треугольник, квадрат и круг разными способами.

Рисунок 3. Перебор вариантов расположения геометрических фигур

Комбинаторные задачи развивают логическое мышление школьников. Решая их обучающиеся овладевают действиями анализа, так как школьникам необходимо выявить существенные признаки устанавливаемых на множестве отношений: играет роль порядок расположения элементов или нет, могут ли повторятся цифры в числе или нет.

При решении задач с помощью построения таблиц умладшие школьники овладевают действием синтеза, так как ученикам приходится соединять элементы в единое целое, достраивать таблицы в соответствии с условием задачи.

Решая комбинированные задачи в начальном курсе математикиформируются действия моделирования, так как, решая комбинированную задачу, обучающемуся необходимо перейти от текста (словесной модели) к решению с помощью вспомогательной модели (графу, таблицы, «дерева вариантов») или к упорядоченному перебору, что формирует умения оперировать образами, вести рассуждения на уровне логических абстракций [2].Отметим, что наиболее удачным методом решения  комбинаторных задач считается  решения с помощью графических и табличных моделей. Они достаточно конкретны, наглядны, что даёт обучающимся зрительно воспринимать и видеть внутренние связи между элементами множества, заданных в  условии задачи.

Формирование познавательных универсальных учебных действий у обучающихся начальных классов  в процессе решения комбинаторных задач на уроке математике приводит к развитию способностей самостоятельно усваивать новые полученные знания, овладевать умениями, т.е. умение учиться.

Таким образом, одним из эффективных средств развития познавательных универсальных учебных действий являются комбинаторные задачи. Использовав комбинаторные задачи в начальном курсе математикиможно достигнуть тех результатов, которыми младший школьник должен овладеть к концу 4-го класса.