Выбор оптимального плана производства молочного коктейля с целью максимизации прибыли

В статье формулируется задача максимизации прибыли для реальной торговой фирмы. Задача решается с применением линейного программирования.

Фирма производит 2 вида молочного коктейля: ванильный и клубничный. Для изготовления коктейля используются три исходных продукта: молоко, мороженное и добавки, расходы которых на одну большую ёмкость коктейля и суточные запасы даны в табл. 1.

Таблица 1.

Расход исходных продуктов для производства одной ёмкости коктейля

Розничная цена за 1 большую ёмкость ванильного молочного коктейля 1000 рублей, а клубничного коктейля 1200 рублей. Какое количество молочного коктейля каждого вида должна производить фирма, чтобы получить максимальную прибыль?

Для решения данной задачи применим линейное программирование [2]. Линейное программирование – наука о методах исследования и отыскания экстремальных значений линейной функции, на неизвестные которой наложены линейные ограничения. Математическая модель задачи [3]:

Пусть Х1 – кол-во ёмкостей ванильного молочного коктейля, Х2-кол-во ёмкостей клубничного молочного коктейля, тогда получаем функцию прибыли:

L(X) =1000X1+1200X2→max

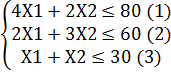
X1≥0; X2≥0

Так как задача имеет только две неизвестных, решим её графически (рис.1).

Рисунок 1. Графическое решение задачи

Областью допустимых решений задачи является выделенная область OABD, С – вектор градиента функции прибыли, линия 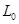 - линия уровня. Точка максимума – точка B, которая является пересечением двух прямых (1) и (2), следовательно, её координаты даются системой:

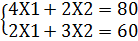
Получили координаты точки В (15; 10), в которой и будет оптимальное решение т.е. Хорt (15;10)

Максимальная суточная прибыль фирмы:

Lmax=1000*15+10*1200=27000 рублей/сутки.

Таким образом, при данных ресурсах максимальная прибыль 27000 рублей в сутки, для этого фирма должна выпускать 15 ёмкостей ванильного молочного коктейля и 10 ёмкостей клубничного.

Для оценки дефицитности ресурсов составим двойственную задачу:

S(y)=80Y1+60Y2+30Y3→min

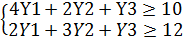
Y1,2,3≥0

Из второй теоремы двойственности о связи решений исходной и двойственной задачи получаем:

Yopt(75;350;0);

Проверка:

S(y) =80*75+60*350+30*0= 27000 рублей.

Таким образом, экстремальные значения функций цели исходной и двойственной задачи совпали, значит двойственная задача решена верно. У3=0, значит, третий ресурс ценности не представляет, а представляют ценность первый и второй ресурсы, причём второй самый ценный.

Результаты решения данной задачи имели практическое применение [1].