Задача оптимизации взаимодействия продавца и рынка с применением теории игр

В статье формулируется задача предварительного маркетингового исследования для реальной торговой фирмы, что делается с целью максимизации предполагаемой прибыли. Задача решается с применением теории матричных игр и линейного программирования.

Прежде чем принять решение о завозе нового товара любая солидная торговая фирма должна провести маркетинговое исследование. В маркетинговых же исследованиях довольно часто применяется теория матричных игр. Роль одного из игроков играет сама фирма, роль другого – конъюнктура рынка и спрос покупателей.

Теория матричных игр находится в тесной связи с линейным программированием, так как каждая конечная игра двух лиц с нулевой суммой может быть представлена как задача линейного программирования и решена симплексным, а в более простом случае графическим методом, и наоборот, задача линейного программирования может быть представлена как игра [2].

Рассмотрим небольшую задачу оптимизации взаимодействия торговой фирмы с рынком или задачу предварительного маркетингового исследования.

Торговая фирма может завести для продажи в различных пропорциях товары четырёх типов – А1, А2, А3 и А4. Их реализация и доход фирмы зависят от вида товара и состояния спроса. Предполагается, что спрос может иметь два состояния – В1 и В2. Данные о прибыли, которая может быть получена от продажи товаров при различных состояниях спроса представлены матрицей А (a_ij(руб.) – прибыль на вложенный рубль, i- номер товара, j –номер состояния спроса).

А=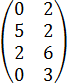

Задача:

Определить оптимальные пропорции завоза товаров из условия максимизации средней прибыли.

Решение:

Применим теорию игр. Роль первого игрока- игрока А будет играть фирма, а роль второго игрока – игрока В – объективные обстоятельства, то есть спрос. Матрица А будет играть роль платёжной матрицы. Строки матрицы будем рассматривать как стратегии первого игрока, столбцы – как стратегии второго.

Из игры можно исключить стратегии. соответствующие первой и четвёртой строкам, назовём их А1 и А4, которые хуже стратегии А3, т.е. стратегии третьей строки. Другими словами, при всех состояниях спроса первый и четвёртый виды товаров не следует завозить, так как они обеспечивают прибыль на вложенный рубль меньшую, чем третий вид товара. Платёжная матрица упрощенной игры имеет вид:

А=  Определим верхнюю и нижнюю цены игры β и α (минимакс и максимин)(таблица 1):

Таблица 1.

Нижняя и верхняя цены игры не равны, значит оптимальное решение игры следует искать среди смешанных стратегий. Обозначим наборы вероятностей чистых стратегий игроков  и .

Сведём игру относительно объективных обстоятельств, а точнее второго игрока – спроса к задаче линейного программирования:

,где ,

ν – цена игры или средняя прибыль на вложенный рубль.

Задача линейного программирования в отнормированных на цену игры переменных выглядит следующим образом [3]:

                                                                                                        (1)

Так как задача (1) имеет только две неизвестных, решим её графически (рис.1).

Рисунок 1. Графическое решение задачи (1)

Областью допустимых решений задачи является выделенная область OABD, вектор градиента функции  является биссектрисой координатного угла, линия  – линия уровня. Точка максимума функции  – точка B, которая является пересечением двух прямых, следовательно, её координаты даются системой:

Получается 

, цена игры – она же средняя прибыль на вложенный рубль – .

Вероятности применения вторым игроком его чистых стратегий, они же вероятности состояний спроса:

, .

Следовательно, набор стратегий второго игрока – спроса , т.е. спрос 1-го типа будет иметь место с вероятностью 0,57, спрос второго типа – с вероятностью 0,43.

Для первого игрока – торговой фирмы составляем двойственную задачу:

где  ,.

                                                                                                               (2)

Решение задачи (2) даётся решением системы:

.

Вероятности применения первым игроком его чистых стратегий, они же пропорции завоза фирмой товаров второго и третьего типа:

, .

Таким образом, полный набор стратегий первого игрока – торговой фирмы .

Таким образом, для продажи следует завозить товар второго и третьего типа в соотношении 57 %:43% от общего объёма товара, а товары первого и четвёртого типов завозить, вообще не следует. При этом средняя прибыль на вложенный рубль ν составит 26/7 или 3,71 руб.

Данная задача представляет собой фрагмент маркетинговых исследований для реальной торговой фирмы [1] и её решение имело реальное практическое применение.