Методические особенности изучения дробей и долей в начальном курсе математики

Methodological peculiarities of studying fractions and fractions in the initial mathematics course

Anna Polshakova,

student, Stavropol state pedagogical institute, Russia, Stavropol

Kristina Popravka,

student, Stavropol state pedagogical institute, Russia, Stavropol

Julia Bruslavtseva,

student, Stavropol state pedagogical institute, Russia, Stavropol

Аннотация. В работе рассмотрены задачи, которые помогут учителю начальной школы  подробно и наглядно ознакомить учащихся с дробями и долями с помощью практико-ориентированных задач и выполнения практических действий над реальными объектами действительности.

Abstract. The paper discusses tasks that will help the primary school teacher clearly and in detail to familiarize students with fractions and fractions with the help of practice-oriented tasks and perform practical actions on real objects in reality.

Ключевые слова: доли; дроби; математика; начальная школа; практико-ориентированное обучение.

Keywords: fraction; fractions; math; elementary school; practice-oriented training.

В период обучения математике в начальной школе учитель должен провести работу по подготовке учащихся к изучению дробей в 5 и 6 классах. Для этого ему необходимо создать все благоприятные условия и подготовить понятный и подробный материал для получения учениками представлений о долях и дробях, чтобы школьники могли использовать полученные знания в дальнейшем. Так, к концу обучения в начальной школе учащиеся должны овладеть следующими навыками [1, с. 259]:

- записывать, показывать и называть доли и дроби по заданной графической модели (прямоугольник, круг, отрезок и др.) или модели объекта действительности (яблоко, пицца, торт и т.д.);

- сравнивать доли и дроби с опорой на рисунок и без него;

- находить доли делением объекта на равные части;

- решать задачи на нахождение доли числа и числа по доле;

- читать и записывать доли в виде дроби со знаменателем, не превышающим числа 10;

- уметь находить дробь от числа и восстанавливать целое число по известной его дроби (обратная операция)

- пользуясь записью дроби, сказать, на сколько равных частей, долей разделена величина и сколько таких частей взято.

Все вышеназванные вопросы рассматриваются в начальной школе на наглядной основе.

Несмотря на то, что доли и дроби присутствуют во всех современных учебно-методических комплексах, именно эта тема до сих пор остается наиболее сложной для учащихся и вызывает у них определенные трудности наряду с элементами геометрии. Поэтому педагог должен больше пользоваться дидактическими материалами по этой теме и использовать игровые методики с применением наглядных материалов.

Отметим, что дроби и доли появляются в результате деления какого-либо объекта действительности (квадрат, круг, отрезок, фрукты, овощи и т.д.) на определенные равные части, поэтому считаем важным использование практических заданий, связанных с этим действием [2]. Вспомним, что доля – это каждая из равных частей единицы, а дробь – это число, которое состоит из одной или нескольких частей единицы [4, с. 338]. Дроби являются логическим продолжением изучения долей: так, вначале изучения этой темы учащиеся сначала учатся делить объекты на равные части, получая, тем самым одинаковые доли, а далее работать с дробями, которые показывают сколько рассматривается равных долей.

Далее приведем примеры заданий на доли и дроби и опишем методические особенности работы с ними.

Задание 1. Используя вспомогательный рисунок круга, разделенного на несколько равных частей, назовите словесное описание полученной части.

Рисунок 1. Круги, разделенные на одинаковые части

Задание 2. Мультипликационные герои Симка и Нолик решили съесть по одному торту. Педагог показывает детям изображение торта, как на рисунках 2 и 3.

Вопросы к рисунку 2:

1. На сколько частей разрезан торт? (Ученики могут сказать, что торт разрезан на 6 частей, так как двух кусочков уже нет. Преподавателю нужно объяснить детям, что те кусочки, которых не хватает, Симка уже съела, а значит, что торт был разделен на 8 частей). Учащиеся должны понять, что при делении круга (торта) на восемь равных частей, каждая из восьми частей есть 1/8.

2. Сколько кусочков торта съела Симка? (2)

3. Сколько кусков торта осталось? (6)

4. Какую часть от всего торта съела Симка? (2/8)

5. Какая часть всей торта осталась? (6/8)

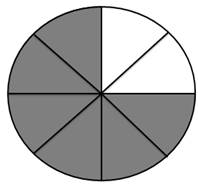
Рисунок 2. Торт, который собиралась съесть Симка

Вопросы к рисунку 3:

1. На сколько частей разрезали торт? (6)

2. Сколько кусков  торта съел Нолик? (1)

3. Сколько кусков осталось? (5)

4. Какую часть от всего торта съел Нолик? (1/6)

5. Сколько частей торта осталось? (5/6)

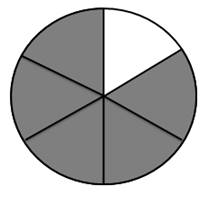
Рисунок 3. Торт, который собирался съесть Нолик

С помощью данного задания, ученики начальных классов овладевают умениями записать доли и дроби, используя вспомогательный рисунок (графическую модель) и сравнивать их, путем наложения соответствующих изображений. Так, сравнив оба рисунка, учащиеся могут прийти к выводу, что 2/8 больше, чем 1/6.  

Помимо правильной записи, ученики начальных классов должны грамотно давать словесное описание полученной части, опираясь на вспомогательный рисунок: одна восьмая, две восьмых, одна шестая и т.д.

Задание 3. Длина подарочной ленты составляет 21 см. От ленты отрезали одну треть. Сколько сантиметров ленты отрезали?

Данная задача является типовым заданием на нахождение доли от заданной величины. Ее смысл заключается в том, что ученику необходимо найти долю реального объекта, что и является по своей сути практическим обучением. Для наглядности ученики чертят в тетради отрезок длиной 21 см (вспомогательную модель реального объекта действительности). Повторяют способ действия для получения одной трети (доли) объекта: разделим вспомогательный чертеж на три равные части, записывая, соответственно, в тетради: 21: 3 = 7 см, и измеряют полученную третью часть, выполняя, таким образом, проверку полученного результата.

Логическим продолжением данного вида заданий являются задачи на нахождение дроби от числа, например, как следующее задание.

Задание 4. Приближается самый главный праздник в году. Бабушка с внучками отправились на елочную ярмарку. У них было 4200 рублей. На покупку красивой елки они потратили 6/7 всех денег. Сколько денег у них осталось после покупки елки?

Особая трудность при изучении дробей и долей заключается в том, что дети с большим трудом сравнивают разные дроби. Следующее задание направлено на формирование этого навыка.

Задание 5. Сравнить дроби 2/4 и 3/4 .

Алгоритм решения:

1. Изобразить 2 одинаковых квадрата.

2. Разделить первый квадрат на четыре равные части и закрасить 2 из них (рис. 4). Записываем соответствующую дробь: 2/4.

Рисунок 4. Изображение 2/4 квадрата

3. Разделить второй квадрат на четыре части и закрасить 3 из них (рис. 5). Получится дробь 3/4.

Рисунок 5. Изображение 3/4 квадрата

4. Сравнивая визуально или путем наложения вспомогательных моделей друг на друга, ученики начальных классов делают выводы о том, что 2/4 < 3/4 или 3/4 > 2/4. При этом педагогу необходимо добиваться правильной формулировки от учащихся: две четвертых меньше, чем три четвертых, а три четвертых больше, чем две четвертых.

Следует отметить, что в процессе решения заданий на доли и дроби учащимися используются разные модели (геометрические, графические, вспомогательный чертеж к задаче и т.д.). Таким образом, решение заданий данной темы помогает развивать у младших школьников навыки моделирования [3], что позволяет говорить о формировании не только предметных, но и метапредметных результатов обучения, заложенных в федеральном государственном образовательном стандарте начального общего образования, как одно из требований к образовательному процессу.